快速排序使用分治法(Divide and conquer)策略来把一个序列(list)分为两个子序列(sub-lists)。
分治法的基本思想是:将原问题分解为若干个规模更小但结构与原问题相似的子问题。递归地解这些子问题,然后将这些子问题的解组合为原问题的解。
算法步骤
- 从数列中挑出一个元素,称为 “基准”(pivot)
- 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作
- 对 “基准” 左边和右边的两个子集,不断重复第一步和第二步,直到所有子集只剩下一个元素为止。
动画演示
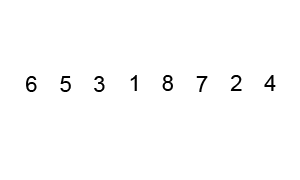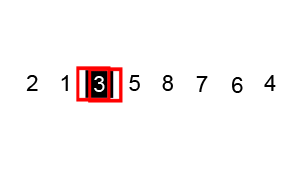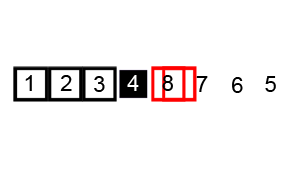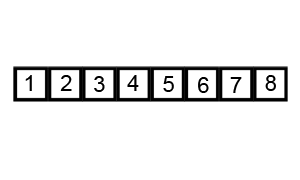
Lua 实现
local function partition(list, low, high)
local low = low
local high = high
local pivotKey = list[low] -- 定义一个中介值
-- 下面将中介值移动到列表的“中间”
-- 当左索引与右索引相邻时停止循环
while low < high do
-- 假如当前右值大于等于中介值则右索引左移
-- 否则交换中介值和右值位置
while low < high and list[high] >= pivotKey do
high = high - 1
end
list[low], list[high] = list[high], list[low]
-- 假如当前左值小于等于中介值则左索引右移
-- 否则交换中介值和左值位置
while low < high and list[low] <= pivotKey do
low = low + 1
end
list[low], list[high] = list[high], list[low]
end
return low
end
local function quickSort(list, low, high)
if low < high then
-- 返回列表中中介值所在的位置,该位置左边的值都小于等于中介值,右边的值都大于等于中介值
local pivotKeyIndex = partition(list, low, high)
-- 分别将中介值左右两边的列表递归快排
quickSort(list, low, pivotKeyIndex - 1)
quickSort(list, pivotKeyIndex + 1, high)
end
end
local list = {
-81, -93, -36.85, -53, -31, 79, 45.94, 36, 94, -95.03, 11, 56, 23, -39,
14, 1, -20.1, -21, 91, 31, 91, -23, 36.5, 44, 82, -30, 51, 96, 64, -41
}
quickSort(list, 1, #list)
print(table.concat(list, ", "))
值得注意的是 Lua 自带的table.sort就是使用的快排,性能肯定比这个纯 Lua 的版本要好